| The
numerals from 441 to 99 except the multiples of ten show this type
of relationship amongst their constituents. |
| (iv)
The constituents may be connected by the particles no `and’ In such
a construction, each of the constituents may in turn enter into different
relationships mentioned in column (i) and (ii) above, as in : |
| akh
`hundred’ no `and’
lakh¸ģ `onč akhénolakh¸ģ
`one hundred and one’ |
akhč
`hundred’ no `and’
cöFé `ten’ + lakh¸ģ `one’
akhčno c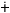 Fé
lakhģ `one hundred and eleven. Fé
lakhģ `one hundred and eleven. |
akhč
`hundred’ x kini `two’ no and cö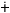 Fé
`ten’ + lakhģ `one’ akhčkinino c Fé
`ten’ + lakhģ `one’ akhčkinino c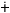 Fé
lakhģ `two hundred and eleven. Fé
lakhģ `two hundred and eleven. |
| The
numerals from 101 to 9999 except the multiples of 100 upto 1000 show
this type of relationship amongst their constituents. The place of
the particle no `and’ however differs, for instance, |
| (a)
In the case of numerals upto 999, it occurs after the place of
hundreds, as in : |
| akhčnomuku |
`one
hundred and twenty’ |
akhčno
c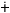 Fé
lakhģ Fé
lakhģ |
`one
hundred and eleven’ etc. |
|
|
| (b)
In the case of numerals beyond one thousand, the particle no `and’
occurs after the place of thousand provided |
| (a)
The place of tens and units have zeros or |
| (b)
The place of hundred has a zero, as in : |
| khčthonhe
lakhģ no akhč lakhģ |
`one
thousand one hundred’ |
| khčthonhe
lakhģ no lakhģ |
`one
thousand and one’ |
khčthonhe
lakhģnoc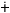 Fé Fé |
`one
thousand and ten’ |
|
|
| (c)
If the place of tens and units have any numeral, the particle no `and’
occurs after the place of hundreds, as in : |
khčtonhe
lakhģ akh č noc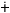 Fé Fé |
`one
thousand one hundred and ten’ |
| khčtonhe
lakhģ akhč lakhģ |
`one
thousand one hundred and
eleven’ |
no c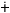 Fé
khakhģ Fé
khakhģ |
|
|
| The
relationship of the various constituents forming a numeral in Sema
may be formalized as follows : |
| |
|
{
B } |
|
| (a) |
D
x B X (A) + D x (A) + P + |
{
C } |
+A |
| |
|
{
B X A } |
|
|
|
| (b)
D x B x A+P+Dx(A) |
| The
limitation in the use of these formula are : |
| (a)
P cannot occur without at least one item preceding and following
i.e., there must be atleast one item on both sides of P and |
| (b)
While the items on either the left or the right side of P can occur
alone without the P, the use of P, however, is obligatory if the items
on both sides of P occur. |
| (c)
In the formula D x B x (A), A can be deleted only if D and B occur
alone, but when in construction with P, it is obligatory to have D
X B X A. |
| The
above would give rise to a total of 35 types of numeral constructions
which are stated below. |
| (a) |
1 |
A
alone1 |
kini |
`two’ |
| |
2 |
B
alone |
c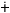 Fé Fé |
`ten’ |
| |
3 |
C
alone |
muku |
`twenty’ |
| |
4 |
D
alone |
akhč |
`hundred’ |
| |
5 |
B
X A |
lhobdģ |
`forty’ |
| |
6 |
B
+ A |
c Fékini Fékini |
`twelve’ |
| |
7 |
C+A |
muku
kini |
`twenty-two’ |
| |
8 |
B
X A + A |
lhobdģ
kini |
`forty
two’ |
| |
9 |
D
X A |
akhč
kini |
`two
hundred’ |
| |
10 |
D
X B |
khčtonhe |
`thousand’s |
| |
11 |
D+B+A |
khčtonhe
kini |
`two
thousand’ |
| |
12 |
D+P+A |
akhčno
lakhģ |
`hundred
and one’ |
| |
13 |
D+P+B |
akhčno
c Fé Fé |
`hundred
and ten’ |
| |
14 |
D+P+C |
akhčno
muku |
`hundred
and twenty’s |
| |
15 |
DXP+BXA |
akhčno
ihobdģ |
`hundred
and forty’ |
|
|
| 1.
The value of A, B, C, D are as under : |
| A
= any numeral from 1 to 9 |
| B
= ten ; |
| C
= twenty or thirty; |
| D
= hundred; |
| P
= particle no `and’. |