| -rh- |
urha: |
�to trap animals� |
-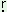 p- p- |
i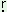 pe pe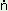 |
�tree-bark� |
-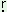 t- t- |
ki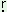 ta: ta: |
�to be of pieces� |
-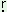 k- k- |
a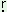 ka: ka: |
�a pitcher� |
-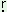 g- g- |
ba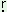 ga: ga: |
�a stick� |
-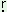 c- c- |
we: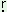 ci: ci: |
�light� (not dark) |
-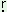 s- s- |
a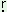 sa: sa: |
�to sneeze� |
-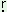 h- h- |
a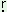 ha: ha: |
�to peel skin� |
| -wk- |
awka: |
�to kill� |
| -wh- |
dawha: |
�path, way� |
| -yp- |
neypa: |
�to smoothen� |
| -yt- |
koyto:r |
�a Gond� |
| -yk- |
uyka: |
�slough of snake� |
| -ys- |
keysar |
�broomstick� |
|
| From the above
charts one could make some observations about the distribution
of the consonant clusters as well as individual consonants.
|
| Out of 20
consonant phonemes there are twelve obstruents and eight sonorants.
Once every consonant in the system combined with every other
consonant we get a total number of 400 two-consonant clusters.
A comparison of the actual clusters with the possible clusters
for each of the four classes of combinations of consonants set
up as follows: |
| (O = Obstruent; S = Sonorant) |
|
Possible Clusters |
Actual Clusters |
| (i) |
O + O (12 x 12) |
144 |
21 |
| (ii) |
S + S (8 x 8) |
65 |
21 |
| (iii) |
O + S (12 x 8) |
96 |
27 |
| (iv) |
S + O (8 x 12) |
96 |
37 |
|
|
------ |
------ |
|
|
400 |
106 |
|
|
------ |
------ |
|
|
This indicates that consonant clusters of class (iv), i.e., sonorant plus obstruent clusters, are more in number.
|
|
The combinational freedom of each consonant can be measured in terms of number of other consonants that it combines with, either as a first member or as a second member. The following table will serve as an index of the relative freedom of or restriction on the occurence privileges of individual phonemes in two-consonant clusters.
|