| 2.2.1.
Indefinite |
| Attributes
of measurement which cannot be counted because of either their unbroken
nature or the impossibility of determining exact number form the indefinite
adjectives. |
| Example
- |
ak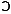 n n
|
‘someone’
|
az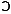 nė nė
|
‘few’
|
dék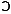
|
‘many/much’
|
|
|
| 2.2.2.
Definite |
| Definite
quantity of a thing is always expressed in units. These discrete quantities
are adjectives of quantity. The cardinal numbers from one to ten,
however, do not enter into construction with the qualified noun, but
through the particles which are known as classifiers or numerical
definitive and denote the nature of the object enumerated. The classifier
numeral combination invariably follows the noun qualified. |
| Example
- |
|
eki
|
ad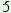 rk rk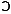
|
‘one dog’
|
|
kitab
|
darńik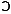
|
‘two books’
|
|
|
| 2.3.
Numerals |
| Numerals
form a subclass of definite adjectives. The numerals from one to ten
are stem forms and from eleven onwards are formed by compounding the
base forms from one to ten. There are two types of numerals viz.,
|
| (a)
Cardinals |
| (b)
Ordinals |
| 2.3.1.
Cardinals |
| There
are, in total, five processes of formation of cardinal numerals. |
| (a)
Base forms |
įk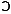
|
‘one’
|
|
įnńi
|
‘two’
|
|
įum
|
‘three’
|
|
įppi
|
‘four’
|
į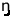 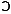
|
‘five’
|
įppė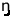
|
‘six’
|
|
kļnļd
|
‘seven’
|
|
pķńi
|
‘eight’
|
ińi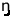
|
‘ten’
|
lļ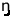 k k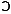
|
‘hundred’
|
|
|
| (b)
Subtraction |
p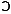 na na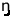
|
‘nine’
|
(10-1=9)
|
|
|
| (c)
Addition |
|
|
‘eleven’
|
(10+1)
|
|
|
‘twelve’
|
(10+2)
|
ińi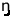 k k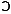 laNįum laNįum
|
‘thirteen’
|
(10+3)
|
|
|
| (d)
Multiplication |
ińi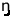 įnńik įnńik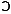
|
‘twenty’
|
(10x2)
|
ińi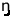 įumk įumk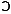
|
‘thirty’
|
(10x3)
|
ińi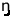 įppik įppik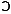
|
‘forty’
|
(10x4)
|
lļńi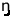 k k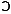
|
‘thousand’
|
(100x10)
|
|
|
| (e)
Multiplication & addition |
|
|
‘twentyone’
|
(10x2+1)
|
|
|
‘twentytwo’
|
(10x2+2)
|
|
|
| 2.3.2
Ordinal numerals : |
| Ordinals
denote position in a numerical series. These are of two types - (a)
fractions (b) non-fractionals. |
| 2.3.2.1
Fractions : |
| Fractional
ordinals are formed by adding /-tąki/ ‘to divide’ or ‘to share’. All
functional ordinals are compound forms. |
| Examples
: |
tąkpļ d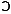 įk įk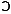
|
‘one fourth’
|
(tąki + įpļ + dė
+ įk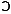 ) )
|
|
|
share + four + ten
+ the
|
|
|
|