3.2.3.
|
Numerals
|
The numerals in this language
were defined as belonging to that grammatical class which on the
paradigmatic axis is capable of taking ordinal suffixes but incapable
of taking number or tense marker and on the syntagmatic axis, is
capable of forming construction with post positions and/ or fill in
the slots of a noun or function as a satellite in a NP. A few example
would illustrate this.
|
| |
| duytor |
‘second’ |
| duybi |
‘two also’ |
| sari pora duy dibi |
‘please give two out of four’ |
| duy lora jayse |
‘two boys went’ etc. |
|
Sub-classification:
|
The numerals in this
language can in the first instance be sub grouped into two, viz.,
simple number word and compound number words. The simple number words
are those that are monomorphemic, i.e., not further analysable into
component parts and the compound number words are those that are
constructed from two or more simple number words. The simple number
words are designated as primary numerals and the compound number words
are designated secondary numerals.
Whereas the primary numerals are a closed set of limited numbers, the
compound number words are infinite. There are only 12 primary numerals
in this language which may be collectively referred to as the terminal
vocabulary of the Naga Pidgin number system. These are listed below.
|
| |
| ek |
‘one’ |
sat |
‘seven’ |
| duy |
‘two’ |
at |
‘eight’ |
| tini |
‘three’ |
n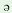 w w |
‘nine’ |
| sari |
‘four’ |
dos |
‘ten’ |
| was |
‘five’ |
noboy |
‘ninety’ |
| choy |
‘six’ |
so |
‘hundred’ |
|
Since the numbers from one to
ten are listed, grouped into ten, and then moves over to listing and
grouping for another ten and so on, it can be stated that the number
system in this language is on the base ten1.
Excepting for the numerals for ninety and hundred, all the numerals
above the ten are secondary ones. The structure of the secondary
numerals can be stated in terms of the relationship of the
constituents amongst themselves. These are discussed below.
1It has also an alternate form having a base
twenty. (Please see the next page).
|
The structure of the secondary
numerals:
|
A secondary numeral in this
language can have a maximum of three constituents. The structure
(relationship of the constituents) the secondary numerals show
different types of permutations and commutations of simple
arithmetic's
viz., summation, subtraction and multiplication. Only the numerals
having three constituents make use of two or more of these devices.
The numerals having only two constituents have either summation or
multiplication but not both. Depending upon the structural device
employed, the secondary numerals in this language can be primarily
sub-grouped into three. These sub groupings along with the illustrative
examples are given below.
|
1. structure showing the
summationof the two constituents:-
|
| |
ba+ro ‘two
+ ten' = baro ‘twelve’ |
| |
te+ro
‘three+ten’ = tero ‘thirteen’ etc. |
| |
|
| |
The numerals1
11 to 18 have the same structure. |
2. The structure showing the
multiplication of the two consituents:-
|
| |
bi X - s
‘two X ten’ = bis
‘twenty’ |
| |
tri X -s
‘three X ten’ = tris
‘thirty’ |
| |
hotu-X-r ‘seven
X ten’ = hotur ‘seventy’ etc. |
| |
The multiples of 10 from 20
to 80 show this type of structure.
|
3. The structure showing the
combinations of summation or subtraction and multiplication:-
|
As mentioned earlier, this
type of structure involves only the secondary numerals having at least
three constituents. In other words, when a numeral has three
constituents, the last two constituents are multiplied in the first
instance and then the value of the first constituent is either
subtracted or summed up as the case may be, with the number arrived at
out of the multiplication. This can be put in a formulaic statement:
|
| |
 |
| |
(a) subracation and
multiplication : |
| |
ontis
‘twenty nine’ = - on +(ti X s) =-1+(3X10)=29 |
| |
onnoys ‘nineteen’
= -onn +(oy-X-s) =-1+ |
| |
(2X10)=-1+20=19 etc. |
1 The
numerals from 11 to 20 and the multiples of ten upto 100 listed in the
next page. |